| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 이지혜
- 조희연
- 픽크루
- 불가피
- 킹덤 고근희
- 미국 금리인하
- 제넥신
- 금리인하
- 유튜버 김재석
- 임영규
- 은혜의 강 교회
- 성남 코로나 확진자
- 스콜피온킹
- 스페인 코로나
- 해킹
- 성남은혜의강교회
- 김재석
- 김영권 아내
- 홍혜걸
- 이상형 만들기
- 고민정
- libtins
- 양적완화
- 학교 개학 연기 4월
- 리리남매
- 뭉쳐야 찬다
- 폰폰테스트
- 최강욱
- 김영권
- 이태원 클라쓰 15회 예고
- Today
- Total
Dork's port
PGP (Pretty Good Privacy) 본문
Phill Zimmermann에 의해 만들어진 서비스
공개키로는 RSA, DSS, Diffie-Hellman이 사용되며, 대칭키로는 CAST-128, IDEA, 3DES가 사용됨.
해쉬로는 SHA-1이 사용된다.
Windows, UNIX, Macintosh 및 많은 운영체제에서 사용 가능하다.
PGP는 4개의 서비스(Authentication, Confidentially, Compression, e-mail compatibility)를 제공한다.
위의 4개의 서비스를 간단하게 다음과 같이 요약할 수 있다.
| Function | Algorithms Used | Descrption |
|
Digital signature |
DSS/SHA or RSA/SHA | SHA-1을 이용해 해쉬코드가 만들어지며, 이 해쉬는 Sender의 Private key를 이용해 DSS나 RSA를 이용해 암호화 됨. |
| Message encryption | CAST or IDEA or Three-key Triple DES with Diffie-Hellman or RSA | Sender에 의해 생성된 one-time session key로 CAST-128, IDEA, 또는 3DES로 암호화 된다. 이 session key는 Diffe-Hellman이나 수신자의 RSA public key암호화 된다. |
| Compression | ZIP | 저장공간이나 전달에 사용하기 위해 ZIP을 이용해 압축을 한다. |
| E-mail compatibility | Radix-64 conversion | e-mail application의 투명성을 제공하기 위해 암호화된 메세지는 Radix-64를 이용해 ASCII로 변환된다. |
많은 E-mail 시스템에서 전송에 ASCII 문자열만 지원하므로 encrypted 된 문자를 전송할때에 문제가 생길 수 있다. 그래서 PGP에서는 Radix-64 conversion을 사용해 이 문제를 해결하였다. Base64와 같은 방법으로 인코딩하며 Radix-64같은 경우엔 optional 24-bit CRC가 =이후에 올 수 있다.
다음으로 나올 표시의 의미는 아래와 같다.
$$k_{s}$$
Session key used in symmetric encryption scheme
$$PR_{a}$$
Private key of user A, used in public-key encryption scheme
$$PU_{a}$$
public key of user A, used in public-key encryption scheme
$$EP$$
Public-key encryption
$$DP$$
Public-key decryption
$$EC$$
Symmentric encryption
$$DC$$
Symmentric decryption
$$H$$
Hash function
$$||$$
concatenation
$$Z$$
Compression suing ZIP algorithm
$$R64$$
Conversion to radix 64 ASCII format
|
#Authentication |
전체적인 알고리즘은 다음과 같다.
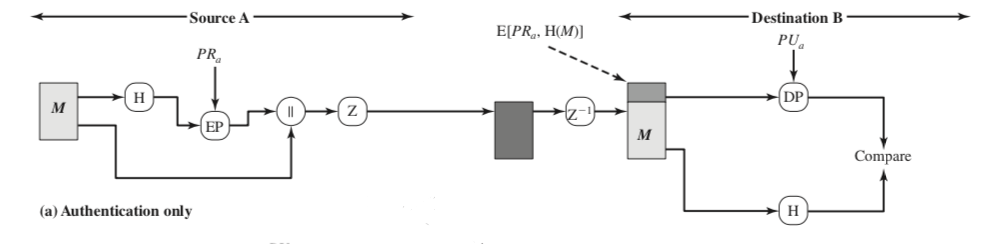
A가 B에게 나는 A다! 라고 말할 필요가 있다고 하자.
이때, PGP에서는 다음과 같은 절차를 따른다.
1. Sender(A)가 메세지를 생성한다.
2. SHA-1을 이용해 메세지에 대한 160bit hash code를 생성한다.
3. Hash code는 Sender(A)의 RSA Private key로 암호화 한다. 그리고 결과를 (1)에서 생성한 메세지의 앞에 붙인다(merge).
4. Receiver(B)는 Sender(A)의 Public key를 이용해 Hash code를 복호화 한다.
5. Receiver(B)가 Sender(A)에게서 받은 메세지 중 Hash code를 제외한 메세지부분을 다시 SHA-1으로 해쉬화 하여 (4)에서 복호화한 Hash code와 비교한다. 비교한 결과 값이 일치하면 수신한 메세지는 A로 부터 송신된 메세지라는 것을 알 수 있다.
위의 상황에서는 Authentication은 보장하지만 메세지에 대한 기밀성(Confidentiality)은 보장하지 못한다(위의 과정에서 메세지는 평문으로 보내졌다). 또한,
|
#Confidentiality |
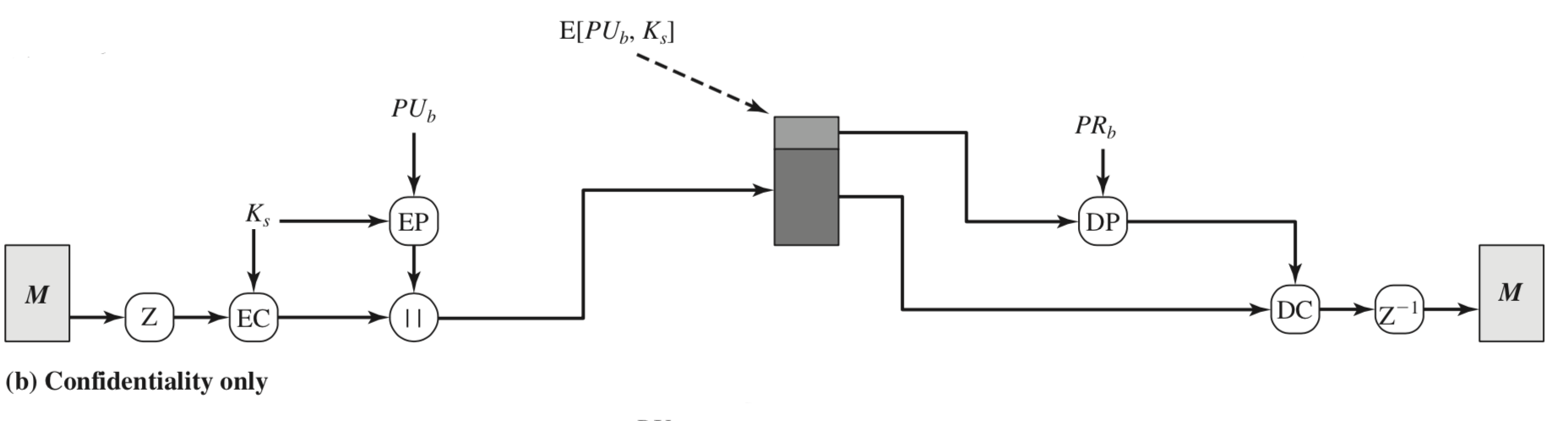
PGP가 가지고 있는 두번째 기능으로는 메세지 전송에 대한 암호화나, 로컬 파일에 대한 암호화에 대한 기밀성이다. 이때 대칭키 암호화 알고리즘인 CAST-128이 주로 사용되며 또한, IDEA나 3DES가 사용 될 수도 있고, 64-bit cipher feedback (CFB) 모드가 사용된다.
CAST-128은 12-16라운드의 Feistel network로 이루어져 있으며 Feistel network는 블록 암호의 일종으로, 암호화 방식이 특정 계산 함수의 반복으로 이루어진다. 이 모델의 장점으로는 암호화 과정과 복호화 과정이 키 순서를 제외한 전체가 같은 계산을 반복하여 라운드 함수가 역연산이 존재할 필요성이 없다. 또한, 64-bit의 block size를 가지며, key size로는 40~128 bits로 이루어 지는데 이때 8-bit씩만 증가한다. 16라운드의 경우 key size가 80bits 이상인 경우 사용된다고 한다.
이때 비대칭키의 키 분배에 관한 문제점을 해결해야하며, PGP에서는 각 대칭키를 한번만 사용한다. 즉, 각 메세지 마다 128-bit의 random한 key가 생성된다. 그리고 그 Session-key(실제로는 one-time key)는 메세지와 함께 전송되며 키의 기밀성을 위해 Receiver의 Public Key로 암호화되어 전송된다.
1. Sender는 128-bit의 Session-key(one-time) key를 생성한다.
2. 메세지는 CAST-128(또는, IDEA나 3DES)로 암호화 한다. 이때, 위에서 생성한 Session-key를 이용한다.
3. Session-Key는 Recipient의 RSA Public Key로 암호화하여 메세지에 첨부된다.
4. Receiver는 자신의 RSA Private Key를 이용하여 Session Key를 복호화 한다.
5. 이 Sesssion Key는 메세지를 복호화하는데 사용된다.
이때, RSA를 사용하시는 대신 PGP는 Diffie-Hellman을 통한 방식도 제공한다.
Diffie-Hellman은 키 교환 방식중 하나로 아래의 조건이 주어졌을때
$$g^a, g^b $$
아래의 값을 구하기 어렵다는 전제로 이루어진 키 교환 방식이다.
$$g^{ab}$$
실제로 PGP에서는 다양한 Elgamal과 같은 Deiffie-Hellman 암/복호화를 지원한다.
암호화 시간을 줄이기 위해 바로 RSA나 ELGamal 암호를 이용해 메세지 암호화는 것 보다 비대칭키와 대칭키의 조합을 이용한다. CAST-128과 다른 대칭키 암호는 실질적으로 RSA나 ElGamal보다 빠르다.
두번째로, 수신자만 seesion-key를 메세지로부터 복호화할 수 있기때문에 session-key 분배 문제를 public-key 알고리즘을 이용하면 해결할 수 있다. e-mail에서는 세션을 계속 유지할 필요가 없기 때문에(전송시에만 연결하고 끊으면 되므로) 세션키 교환에 대한 protocol이 필요가 없으며 게다가, 각 메세지는 one-time key를 사용하므로 store-and-forward nature 방식을 사용하는 e-mail방식에서는 같은 session-key를 같기 위해 handshaking을 사용하는것이 실용적이지 못하다.
마지막으로, Session-key를 일회성으로 사용하는것은 대칭기의 장점을 부각시킨다(보안성이 더욱 증대된다). 적은 길이의 평문이 각 key로 암호화 되며, 키 간 어떠한 연관성도 없다. 그리고 PGP는 768 ~ 3072bits의 key size의 옵션을 제공한다(DSS의 경우 1024 bits가 최대).
|
# Confidentiality and authentication |

위에서 PGP의 인증 및 기밀성에 대한 부분을 살펴보았따.
그렇다면 이 두가지를 한번에 할 수 없을까? 있다!
1. Sender가 메세지를 생성한다.
2. SHA-1를 이용해 메세지에 대한 Hash code를 생성하여 기존의 메세지에 첨부한다.
3. Sender의 Private-key를 이용하여 위의 (2)에서 만든 Hash code를 암호화 한다. (2)를 암호화 한 Hash code와 평문 메세지를 concatenation 한다. ※이때 Receiver가 Sender의 Public-key를 이용해서 복호화에 성공한다면, Authentication이 충족된다.
왜 이때 압축을 하는지 의문이다. 추후에 알아보도록 하자. 모든 과정이 끝난 후 압축을 한다면 조금 더 효율적일 것 같은데 특별한 이유가 있나..? 아래에 이유가 있다!

4. Sender가 Session-key를 생성하여 위의 메세지 전체를 암호화 한다. 그리고, 생성한 Session-key를 Recipient의 public-key를 이용하여 암호화 한다(이때 암호화한 내용은 Recipient의 Public-key에 대응하는 Private-key로만 복호화가 가능하므로 Confidentiality 충족).
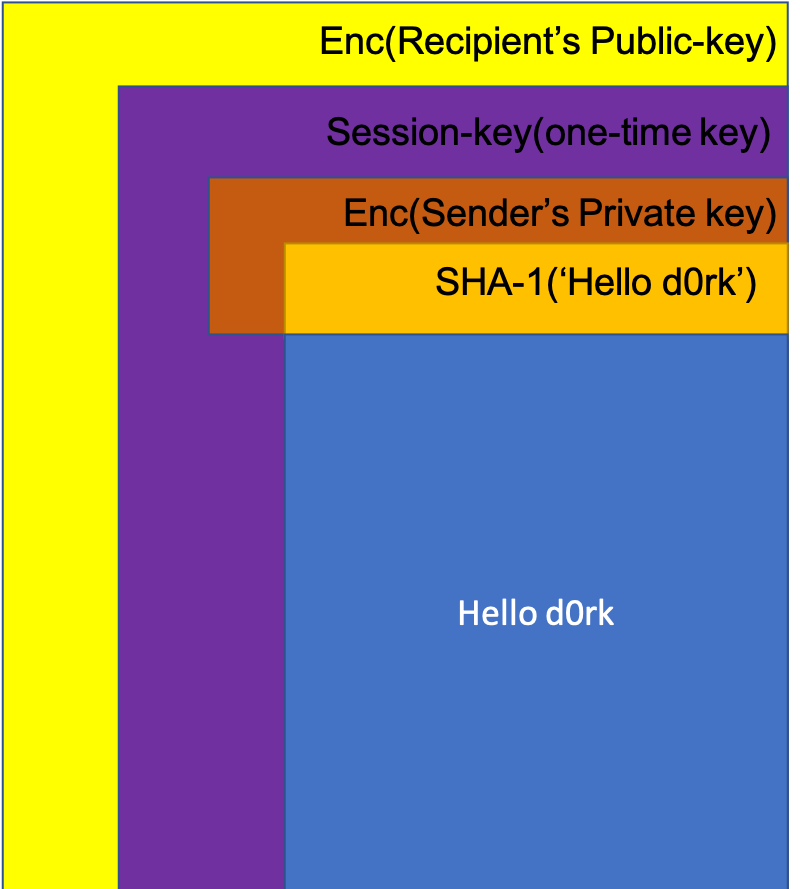
5. 이때 Receiver가 받은 메세지는 위와 같다. 우선 Receiver의 Private-key로 메세지를 복호화를 하면, Session-key를 획득 할 수 있다.
6. (5)에서 얻은 Session-key로 메세지를 복호화 하면 평문의 'Hello d0rk'와 Sender의 Public-key로 복호화 할 수 있는 Hash code에 대한 값을 얻을 수 있다.
7. Sender의 Private-key로 암호화 되어있는 Hash code를 Sender의 Public-key로 복호화 하여 평문 메세지에 대한 Hash code를 복호화한다.
8. (7)에서 얻은 Hash code와 얻은 평문에 대한 SHA-1값을 비교하여 일치하면 Authentication도 보증된다.
|
# Compression |
기본적으로, PGP는 서명 후, 암호화 전 Compression을 한다. 이것은 e-mail 전송과 파일 저장에서 공간을 절약하는 이점이 있다.
서명이 Compression 전에 이루어지는 이유
1. future verification을 위해 압축되지 않은 메세지를 서명과 함께 저장하는 것이 더욱 바람직하다. 만약 압축된 메세지를 서명하는 경우, 확인을 위해 압축된 메세지를 저장하거나 확인을 위해 다시 메세지를 압축해야 하기 때문(서명은 압축된 메세지에 대해 유효하다).
2. 검증을 위해 동적으로 압축된 메세지를 생성하려고 했더라도, PGP의 compression 알고리즘은 다양하다. 다양한 알고리즘 구현은 실행속도와 비율면에서 서로 차이가 있으므로 다른 압축형식이 생성된다(즉, output이 달라진다 == Hash의 결과가 달라진다). 그러나, 어떤 버전의 compression 알고리즘을 을 사용하던 올바르게 압축해제가 되기 때문에 별다른 문제는 없으나, 만약 압축후에 Hash와 서명을 적용하면, 모든 PGP는 동일한 version의 압축을 사용해야 한다(최초에 압축된 알고리즘으로 구현해야 똑같은 데이터 값이 나오고 그래야 Hash가 동일해 지므로 검증을 위해선 같은 압축방식을 사용해야한다).
암호화 전에 Compresssion이 이루어지는 이유
1. 메세지 암호화는 Compression 후에 적용되어 암호학적 보안을 강화시긴다. 이유는 compression된 메세지가 평문 보다 중복이 적기 때문에, 암호 분석이 더욱 어렵다.
PGP는 Compression Algorithm으로는 ZIP이 사용된다.
|
# E-mail Compatibility |
PGP가 적용되면, 전송되는 블록중 일부분 이상 암호화 된다(Authentication을 사용하는 경우 message digest 부분 , Confidentially를 사용하는 경우 messsage와 sign부분). 따라서, 결과 블록의 일부나 전체가 임의의 8-bit octets의 stream으로 구성된다. 그러나 많은 e-mail 시스템은 ASCII text만 지원하므로, 암호화된 부분을 전송하려고 하면 전송에 실패할 수 있다(암호화 된 부분이 ASCII의 범위를 초과할 수 있으므로). 따라서 PGP는 암호화 된 부분을 ASCII로 바꾸는 Radix-64를 제공한다.
3 octets의 이진 데이터는 4개의 ASCII와 대응되며(Base64와 동일), 위에서 언급했듯 오류를 탐지할 수 있는 CRC를 제공한다. 3 Byte를 4 Byte와 대응시키므로 33%의 데이터가 증가된다. Session-key와 Signature 부분이 비교적 작으므로 33%가 증가 되더라도 큰 오버헤드가 일어나진 않으며, 평문은 압축되기 때문에 Radix-64를 사용하여도 평문에 대한 오버헤드 역시 크지 않다(반대로 말하면, 평문에 대한 Compress가 위의 Radix-64의 오버헤드를 상쇄시킬 수 있도록 충분히 압축되어야 한다).
[HELD96]에서 보고한 바에 따르면 ZIP 2.0의 버전의 압츅률은 2.0이므로 Session-key와 Signature부분을 무시한다면 PGP에 대한 데이터 증감은 file 길이 X에 대해 다음과 같이 정리할 수 있다.
$$1.33 * 0.5 * X = 0.665 * X$$
1.33은 Radix-64를 적용한 데이터의 길이이며, 0.5는 ZIP 2.0의 압축률을 적용한 데이터길이이다. 즉, 파일의 길이 X에서 0.6정도로 감소하므로 약 1/3의 데이터 길이가 절약된다. 또한 Authentication을 사용하는 경우, SHA-1부분만 암호화 되는데, 이때 PGP에서는 SHA-1부분만 Radix-64로 인코딩할 수 있다. 이 경우 PGP를 사용하지 않고도 사용자가 평문을 읽을 수 있다는 장점이 있다(이때 서명에 대한 확인은 불가).
PGP의 전체적인 다이어그램은 다음과 같다.

1. 평문 메세지 X
2. Signature가 필요한 경우 X에 Signature를 concatenate하고, 필요 없을 경우 바로 압축
3. Confidentiality가 필요한 경우 session-key를 생성하여, session-key를 이용해 메세지 X를 암호화한 후 session-key를 Recipient의 public-key로 암호화
4. radix-64 적용
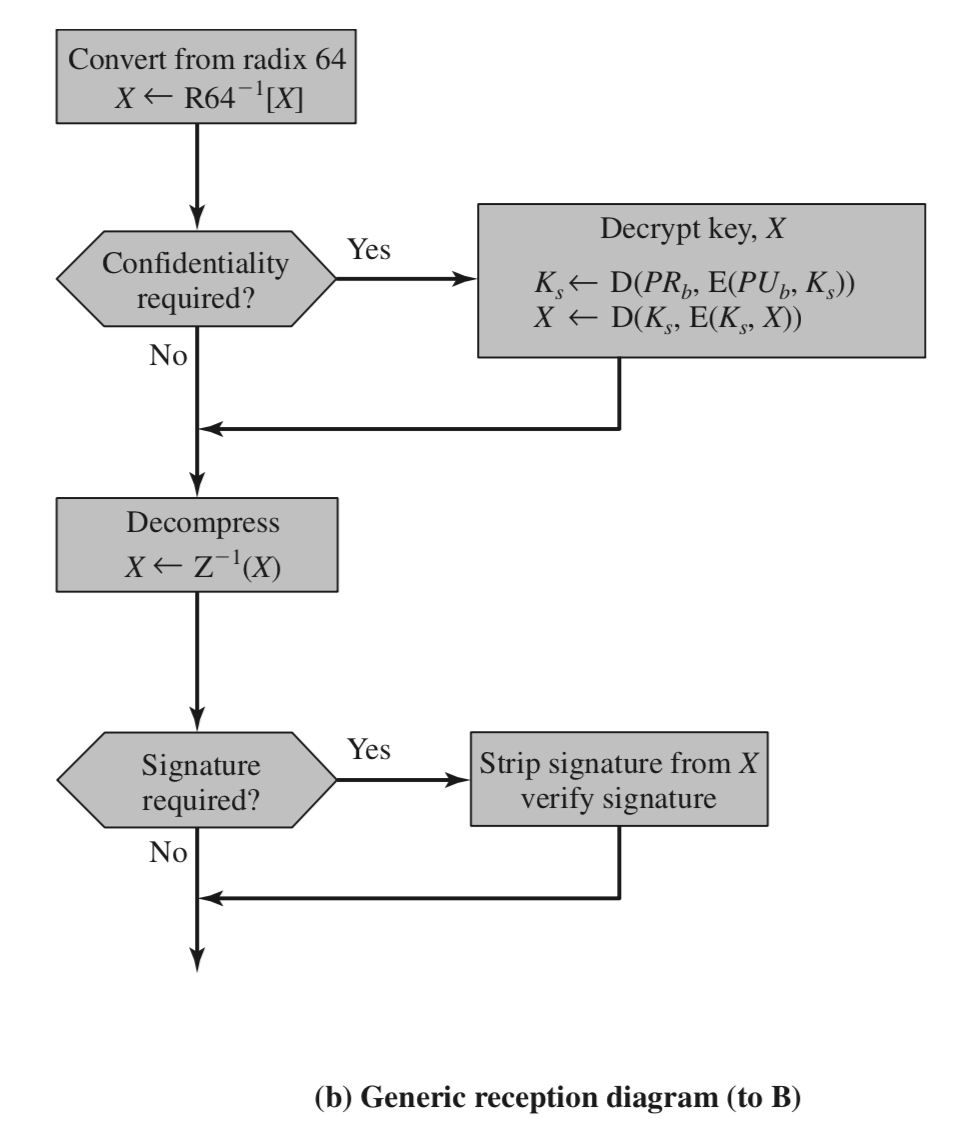
1. Radix-64를 디코딩
2. Confidentiality가 되어있는 경우 자신의 Private-key를 이용해 Session-key를 복호화 그 후, Session-key로 암호화 되어있는 메세지 X를 복호화 한 Session-key를 이용해 복호화
3. Decompress
4. Signature가 필요한 경우 X의 메세지에서 Hash code를 분리하여 일치 여부 확인
끗!! ㅋ
Reference : Cryptography and Network Security, sixth Ed
'Network' 카테고리의 다른 글
| S/MIME (Secure/Multipurpose Internet Mail Extension) - 2 (0) | 2019.04.04 |
|---|---|
| S/MIME (Secure/Multipurpose Internet Mail Extension) - 1 (0) | 2019.04.02 |
| 네트워크 프린터 해킹(Network Printer Hacking) (17) | 2018.04.20 |
| [Network Hacking] Cookie를 이용한 인증 세션 가로채기(Cookie를 이용해 로그인 하기, 네이버 해킹, 다음 해킹) - 2 (1) | 2018.01.08 |
| [Network Hacking] Cookie를 이용한 인증 세션 가로채기(Cookie를 이용해 로그인 하기, 네이버 해킹, 다음 해킹) - 1 (0) | 2018.01.08 |




